1. Arithmetic Coding Example

COMPRESSION ALGORITHMS COMPRESSION ALGORITHMS Some solutions to exercise 5.29 (page 103),. As usual I recommend that you not look at these solutions until you have thought hard about your own. When making your own solution, you may find it useful to have an implementation of the Huffman algorithm. You are welcome to use my perl program or python program. Here are example compression programs, mainly written in C, all designed to compress a. You can download all the programs and a in.

Some notes on an approach using runlength codes Huffman using run lengths In my runlength/Huffman encoder the maximum runlength is 69 for the reasons explained in. I assume the length of the file is known to the decoder; this allows the compressed file to be about 6 bits shorter than if I ensured that the file is self-delimiting in some way, for example, using the EOF character. My encoder is a C program,; the decoder is a perl program, because I didn't want to figure out how to write the decoder in C. I am pretty sure that these programs will work on any files. The usage is RLencode file.RLZ RLdecode.p decoded The encoder gets the file into 831 bits. If the source filelength is changed from 10000, please add the Nmax=blah argument to inform the decoder of the correct filelength.

Thus: RLdecode.p Nmax=10000 decoded Arithmetic coding It's hard to make an arithmetic code that works perfectly. And work on all test files I have tried, but I am still not certain they will always always work!

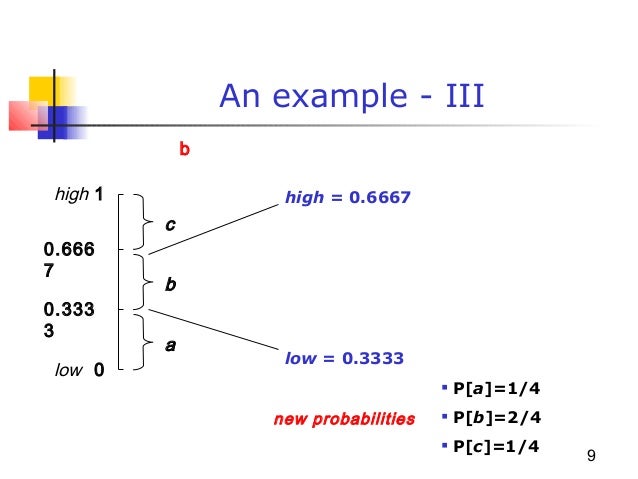
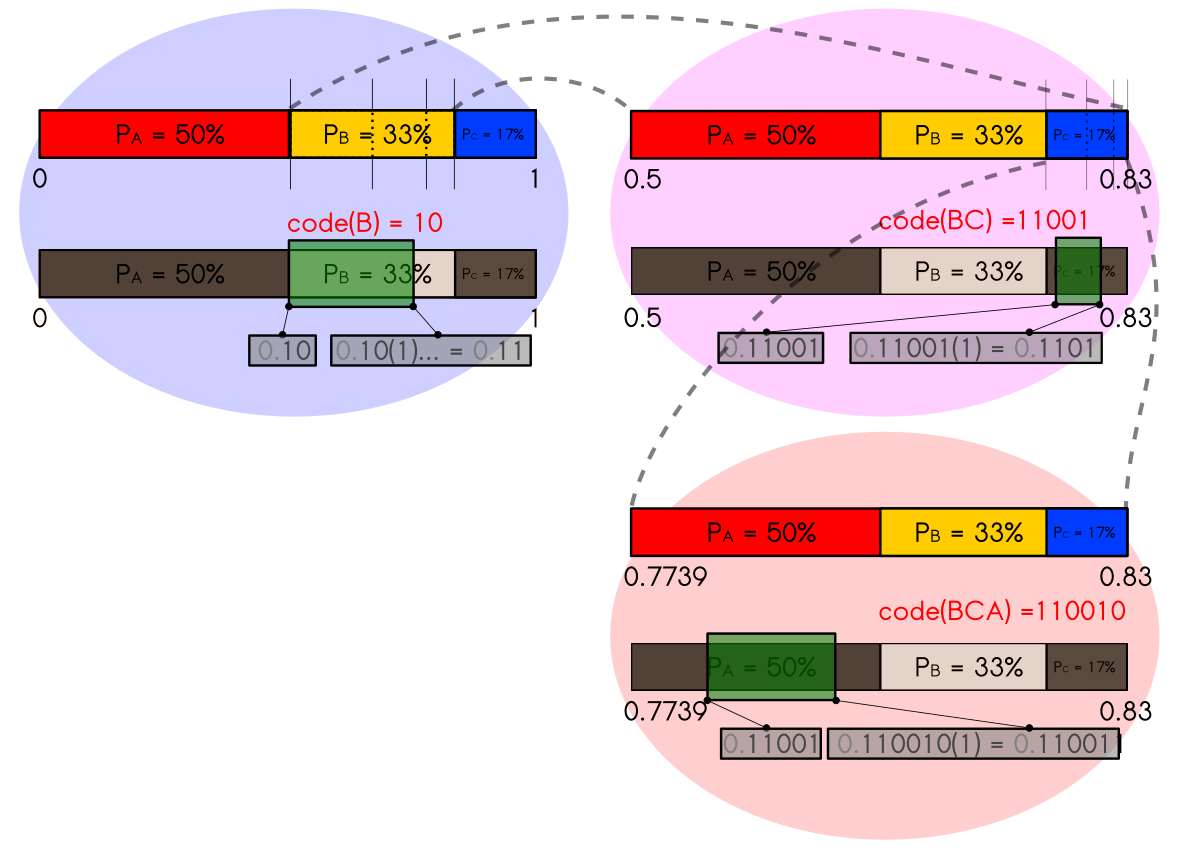
Arithmetic Coding Algorithm Initialize L: = 0 and R: = 1; For i = 1 to n do W:= R – L; L: = L + W.C(x i-1); R:= L + W.C(x i); T: = (L+R)/2; Choose code for the tag C(x i) = P(x 0) + P(x 1) + P(x i). We already mentioned above that the Arithmetic Coding algorithm works sequentially. Thus we need some notion of what the sequential input and output of the encode/decoder might look like. This leads us directly to the notion of a SEQUENCE: DEFINITION 2 (SEQUENCE). A series S = (s1,s2.) of symbols si from an.

(Indeed, I reckon there's a probability of 1/million or so per megabyte of compressed output that this algorithm will get into trouble. For a better-written arithmetic coding algorithm, please see, or.) Arithmetic coding is nice because it lends itself to adaptive models, corresponding for example to the belief that the bias of the bent coin is not known, and should be inferred as we go; or to the belief that the bias of the bent coin might change with time.

The two programs have two choices of compilation options, corresponding to two possible adaptive models. One model (well suited to the competition problem) asserts that the bias of the coin is known to be accurately very close to 0.01; the other asserts that the bias is unknown and could be anything in the ballpark 0.01-0.99. This choice is determined in the file, which is included at compilation time by both programs. The programs are used thus: ACdecode ACencode ACencode file.ACZ ACdecode file.decoded This encoder gets the sparse file into 829 bits. The decoder makes use of the known source file length, N=10000. The results achieved by arithmetic coding are especially impressive for even larger files. For example, I made a million-bit source file using N=1000000 M=10000 million.dat and compared ACencode with the runlength encoder RLencode.

The compressed file lengths were 80797 file.ACZ 81025 file.RLZ Golomb code The Golomb code is a very simple code that is both a runlength code and an approximate arithmetic coder. The encoder has just two adjustable parameters, one bit (here set to 0) which identifies the more probable symbol, and an integer m (here set to 6 or 7) whose value defines the implicit probability of the less probable symbol, via p 1 = ln(2) 2 - m. We define M = 2 m. To encode a file, the Golomb encoder outputs a 1 every time the stream contains M consecutive 0s. Whenever it encounters (for some r between 0 and M-1) a string of r consecutive 0s followed by a 1, it outputs a 0 followed by the integer r encoded as an m-bit binary number.

This encoder may be viewed as a special case of the runlength-based Huffman code with a maximum runlength to be a power of 2, and all runs assigned equal implicit probability. One may also view it as an approximate arithmetic coder; adaptation may be performed by adjusting m. The Golomb coder was the starting point for the Z-coder, an excellent compression algorithm used inside.

The programs are used thus: GolombEncode GolombDecode file.GZ file.decoded This encoder gets the sparse file into 870 bits (when m=7) and 838 bits (when m=6). That's very close to optimal, isn't it! The decoder does not make use of a known source file length; when it hits an EOF symbol, it stops decoding and terminates the file correctly. Code Calpha n traditional binary length calpha(n) 1 1 1 1 2 10 2 010 3 11 2 011 4 100 3 00100 5 101 3 00101 6 110 3 00110.

45 101101 6 1 Run length code with cheap encoder for integers We can make a really small compression algorithm that is reasonably well suited to sparse files by simply counting the run lengths of 1s and 0s, then coding those integers into binary with a simple uniquely decodeable code. The program encodes the runlengths using the code Calpha, described in Chapter 7 of Information Theory, Inference, and Learning Algorithms. (Ch 7: Codes for Integers). The same program can function as an encoder or a decoder; add the command line argument '-1' to select the decoder.

Encoding usage: IRL file.IRLZ decoding usage: IRL -1 decoded This program does not use an explicit probabilistic model; instead, it uses an implicit probabilistic model defined by the chosen codelengths for integers. For example, according to Calpha, the implicit probabilities of 2 and 3 are both 1/8, and the probabilities of 4, 5, 6, and 7 are all 1/32. This program gets the sparse file into 1286 bits.

Further ideas for other solutions Position code plus `bits back' Here's a fun idea. To encode a file of length N=10,000, of which roughly 100 of the bits are 1s, we could encode the position of each of the 1s in the file. Since each position can be represented by a 14-bit integer, the compressed file length will be roughly 100x14 = 1400 bits. Now, that's some way off from the expected Shannon information content, 800 bits or so.

Well, an encoding of all the positions has redundancy in it in the sense that the encoder is free to choose the order of the encoded bit-positions. This freedom means that the encoder has the opportunity to encode not only the 100 bit-positions but also an arbitrary choice of one from the 100! (one hundred factorial) possible permutations.

Arithmetic Coding Example

In order to make that choice, the encoder could sub-contract to his friend Fred, who also wants to communicate over this channel, the decision about the choice of permutation. Receiving the permuted string of bits, the receiver can then deduce not only the sparse file but also Fred's choice. And Fred can use that choice to convey another file of size log 2(100!) bits, which is very roughly 100 (log 2 (100/e) ), or 520 bits. So the net cost of communicating this way is (total transmitted length in bits) - (length in bits of Fred's hidden transmission) = 1400 - 520 = 880 bits. Which is (pretty near) the expected Shannon information content! This idea is called bits-back coding.

We encode in an arbitrary way, that requires some extra bits to resolve the arbitrariness; then claim back the cost of those extra bits by selling them to Fred. Now we get to the really fun bit: can you write a compression method such that the encoder himself plays the role of Fred?

- i.e., the encoder chooses the permutation of the bit-positions in a way that conveys some of the bit-positions! Related concepts. How should Fred turn his 600-bit file into a permutation of the 100 bits?

We need an efficient and practical program. And a decoder that turns a permutation back into bits. A nearby concept is this: imagine that Joe wants to communicate an unordered selection of r objects from N objects.

How should he encode this selection in bits? Last modified: Mon Feb 18 17.

Range Encoder Range encoder Homepage The range encoder is a fast multisymbol entropy coder (similar to arithmetic coding) with GNU general public license (other licenses on request). It's compression is within 0.01% of arithmetic coding. It is based on an article dated 1979, so it is believed to be patent free. The range encoder is an entropy coder similar to the arithmetic coder or huffman coder. Compared to an arithmetic coder the files are minimally larger (less than 0.01% in most cases) but the operation speed is nearly twice as fast. This range coder is distributed for free with GNU general public license. The range encoder is based on an.

Our copyright allows you to make copies of that article for research purposes, however if it is illegal in your country you are not allowed to download that file. If you know the copyright holder please tell me. There also was a poster on the 1998 where (inhouse use only, copyright IEEE) and are available. This package contains building bricks for a compression program. The files are distributed with GNU general public license.

If this doesn't fit your needs (free of charge, availability of source code for your program too) email me at michael@compressconsult.com, I am sure we can arrange. Politics: if you charge I charge - but less than you need to hire a programmer to write & test it. I will not warrant more than your employee would when writing such a program if I charge. I will not warrant anything on the freeware - see the license.

However this coder has been tested on several GB of data during test of my freeware data compression program. I have been told that IBM UK did not apply for any patent on this 1979 range coder method as described in the article, so I have good reasons to claim it patent free.

Having done this legalize stuff, here for the fun part:) Contained in the source archive ( or ) is:. The entropy coder (range coder) source code; this is the only part you need to use the range coder. Files: rangecod.h, rangecod.c.

A fast probability model (qsmodel) doing periodic updates of probability and keeping the total count a power of two. It is used in two of the three example programs. Files: qsmodel.h, qsmodel.c. Three example programs doing a simple static model, an adaptive order 0 model and an adaptive order 1 model. There are available, or use the included makefiele. Auxiliary files: port.h: containing definitions used makefile: a makefile.

text files: readme.txt: do what the name suggests to do examples.txt: closer description of the examples license: GNU general public license, version 2. There is a supplementary file called renorm95.c distributed under different conditions (basically: research purposes) that changes the rangecoder into an arithmetic coder to allow comparisons. It can be downloaded from or for research purposes.

These programs differ in the closing from the ones used to produce the tables in the DCC98 poster so filesize does vary by some bytes. History: (all versions are compatible) 1.2 added some more examples (order 1, simple) 1.3 fixed a bug that could occur when compressing 16MB without resetting and removed references to eiunix.tuwien.ac.at from files. Source code version 1.3 or. Source code for comparing with arithmetic coding; download for research only. Or. Developer studio 5.0 for those who need it. presented on the Data Recording Conference, Southampton, July 1979.

I could not find the copyright holder, but our law allows to make copies for scientific or classroom usage. If it is illegal for you to make or possess such copies don't download. (inhouse use only, copyright IEEE) and of my DCC poster are available. Postcardware My daughter would be pleased to receive stamps from various countries, so if you like please send a postcard to Marion Schindler Billrothstr.

39 A-1190 Vienna Austria - Europe If you have any questions or suggestions regarding range encoding please mail michael@compressconsult.com Compressconsult.com will also assist in adaption to your needs, integration or other data compression related issues. The range coder is a free program of You also might want to look at our or our free compressor.

We also give compression advice or knowhow, see the, Oct. If you locate a spelling error szip and the data.